[BOJ] 1708번: 볼록 껍질(Convex hull)

주소: https://www.acmicpc.net/problem/1708

분야: 계산기하학

N개의 좌표가 주어졌을 때 모든 점을 포함하는 볼록 껍질(Convex hull)을 이루는 점의 개수를 찾는 문제입니다.

현업에서 Convex hull은 영상 내에서 ROI(region of interest)영역을 Segmentation을 하였을 때, 윤곽선을 대략적으로 추출하는 경우 등에 사용할 수 있습니다. (오목한 부분이 존재할 경우에는 사용을 추천하지 않습니다.)

대표적인 Convex hull 알고리즘은 여러 가지가 있습니다. 제가 아는 바로는 그레이엄 스캔(Graham Scan)과 Andrew 알고리즘이 있는데요, 아래 코드는 그레이엄 스캔을 구현한 것입니다.

---

그레이엄 스캔 알고리즘의 대략적인 설명은 다음과 같습니다.

1. 시작점을 찾습니다.

N개의 점 중에서 Y좌표가 가장 작은 점을 선택합니다.

만약 여러 개라면 X좌표가 가장 작은 점을 선택합니다.

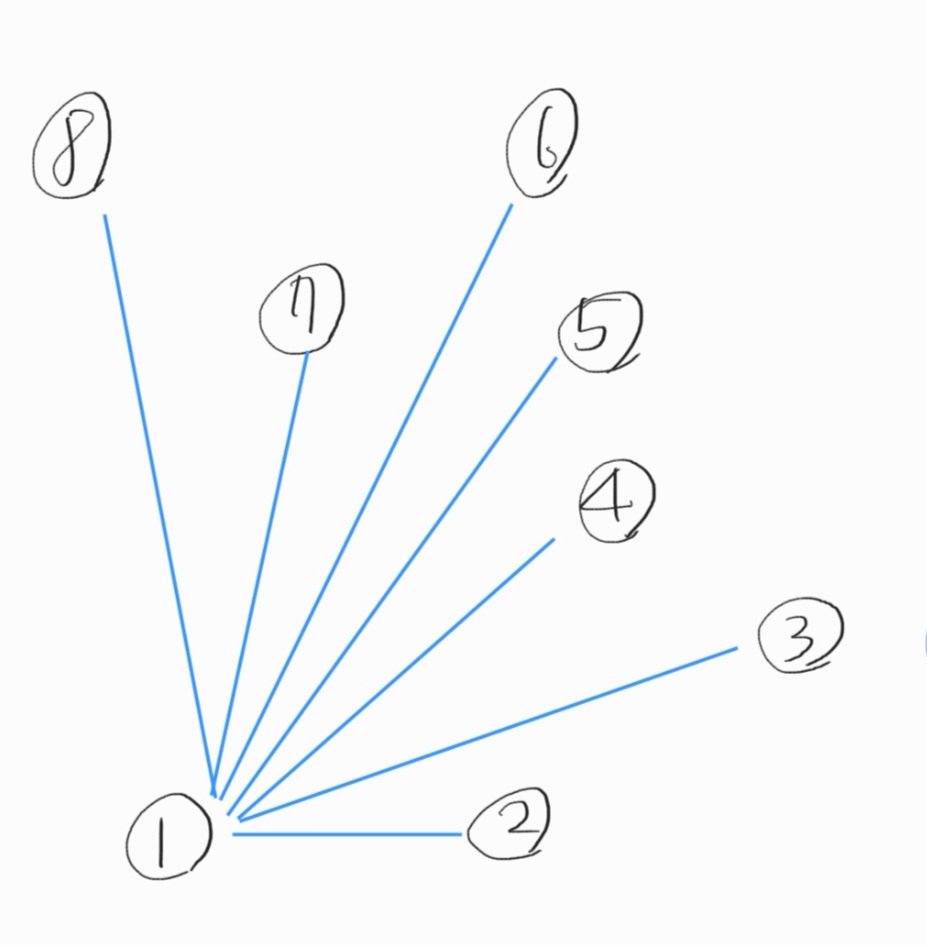
2. 시작점을 기준으로 반시계 방향으로 각도순 정렬합니다. 

각도를 어떻게 재느냐? 가 문제인데요, 정확한 각도를 잴 필요는 없습니다. ccw 방식을 사용하여 각도의 크고 작음을 비교하면 됩니다. 아래 소스에서는 정렬을 위해 퀵정렬을 사용하였고, ccw를 사용하는 comp 함수를 만들어서 각도 비교를 수행하였습니다.

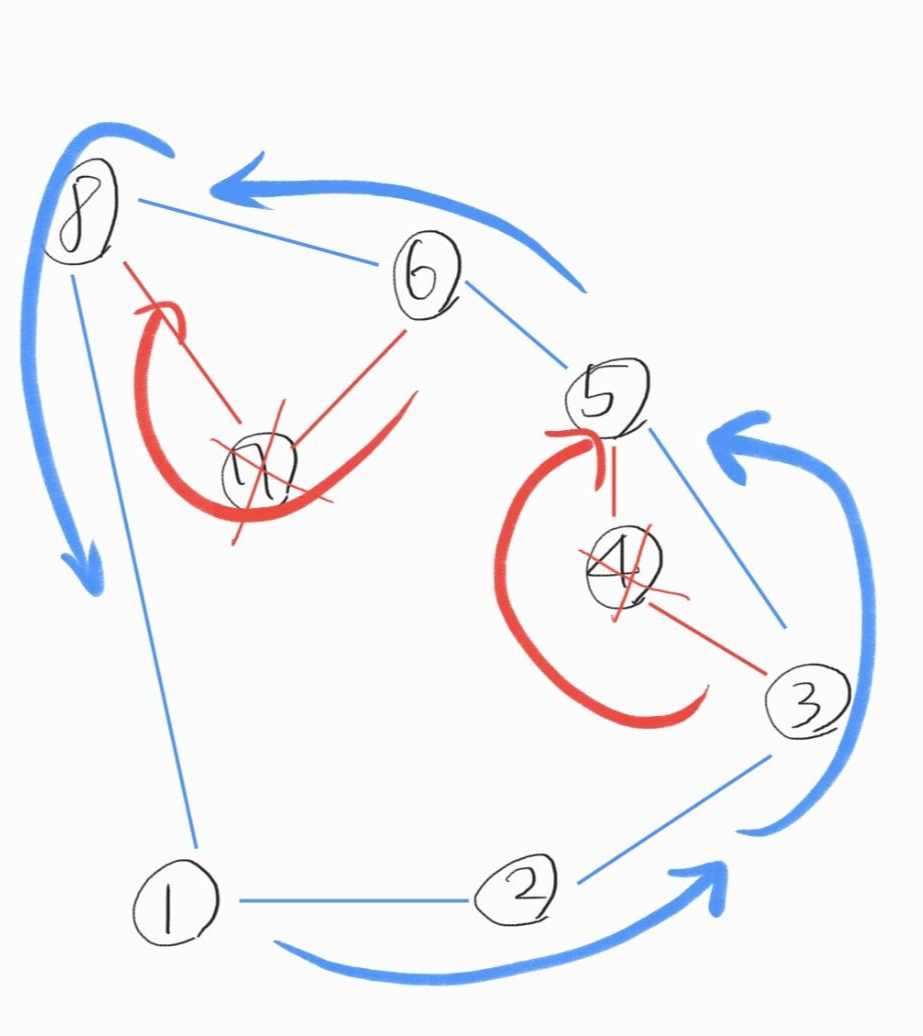
3. 정렬이 끝나면 정렬된 점을 순회하여 반시계 방향일 경우에만 스택에 쌓아갑니다.

이 과정이 처음에는 많이 헷갈립니다. 일단 시작점과 그 다음 점의 좌표를 스택에 넣어줍니다.

그리고 스택에 들어간 최상단 2개의 점과, 3번째 점의 ccw를 계산합니다.

반시계 방향일 경우에는 3번째 점을 스택에 넣습니다. 반시계 방향이 아닐 경우에는 스택을 Pop하고, 다시 ccw를 구합니다. 반시계 방향이 될 때까지 pop을 하며 ccw를 구합니다.

이 과정을 모든 점을 방문할 때까지 반복합니다.

#include <iostream>

using namespace std;
using ll = long long;
const int SIZE = 100000;

struct Point{
	int x, y;
};

Point arr[SIZE + 1];
int stack[SIZE + 1];
int top = 0;

ll ccw(Point p1, Point p2, Point p3)
{
	ll l1 = 1LL * ((ll)p2.x - (ll)p1.x)*((ll)p3.y - (ll)p1.y);
	ll l2 = 1LL * ((ll)p3.x - (ll)p1.x)*((ll)p2.y - (ll)p1.y);
	return l1 - l2;
}

int comp(Point p1, Point p2)
{
	ll res = ccw(arr[0], p1, p2);

	if (res != 0)
		return res > 0;

	if (p1.y != p2.y)
		return p1.y < p2.y;

	return p1.x < p2.x;
}

void QuickSort(int l, int r)
{
	if (r <= l)
		return;

	int i = l;
	int j = r + 1;
	int p = l;

	while (i < j) {
		do { i++; } while (i <= r && comp(arr[i], arr[p]) > 0);
		do { j--; } while (j >= l + 1 && comp(arr[j], arr[p]) <= 0);
		if (i < j) swap<Point>(arr[i], arr[j]);
	}

	swap<Point>(arr[j], arr[p]);
	QuickSort(l, j - 1);
	QuickSort(j + 1, r);
}

int main()
{
	int N, min_idx = 0;
	cin >> N;

	for (int i = 0; i < N; i++) {
		cin >> arr[i].x >> arr[i].y;

		if (arr[i].y <= arr[min_idx].y) {
			if (arr[i].y == arr[min_idx].y) {
				if (arr[i].x < arr[min_idx].x)
					min_idx = i;
			}
			else {
				min_idx = i;
			}
		}
	}

	swap<Point>(arr[0], arr[min_idx]);
	QuickSort(1, N - 1);

	stack[top++] = 0;
	stack[top++] = 1;

	Point p1, p2, p3;
	int idx = 2;
	while (idx < N) {
		while (top >= 2) {
			p1 = arr[stack[top - 2]];
			p2 = arr[stack[top - 1]];
			p3 = arr[idx];

			if (ccw(p1, p2, p3) <= 0)
				top--;
			else
				break;
		}

		stack[top++] = idx;
		idx++;
	}

	cout << (top < 2 ? -1 : top) << endl;

	return 0;
}