영상을 이진화하기 위해 최적의 임계값을 찾는 방법을 알아보겠습니다. 널리 알려진 방법으로는 Otsu와 Triangle method 2가지가 있습니다. 이번 포스팅에서는 Otsu’s method에 대해 소개하려 합니다.
OTSU 알고리즘
영상 이진화를 위한 최적의 임계값을 찾아내는 Otsu 알고리즘은 1979년에 발표되었습니다. 이전 포스팅에서 언급한 것처럼 이진화는 영상을 2개의 클래스(0과 1 또는 0과 255)로 분류하는 것을 의미하는데요, Otsu 알고리즘은 클래스 내에서 분산을 최소화(클래스 내(Inner class; within class)에서는 비슷한 픽셀끼리 모음)또는 클래스 간 분산을 최대화(두 개의 클래스 간(Inter class; between class) 차이를 가능한 크게 함)하여 임계값을 결정하게 됩니다.
수식은 다소 복잡하기 때문에 아래 그림을 활용하여 설명을 하려고 합니다.
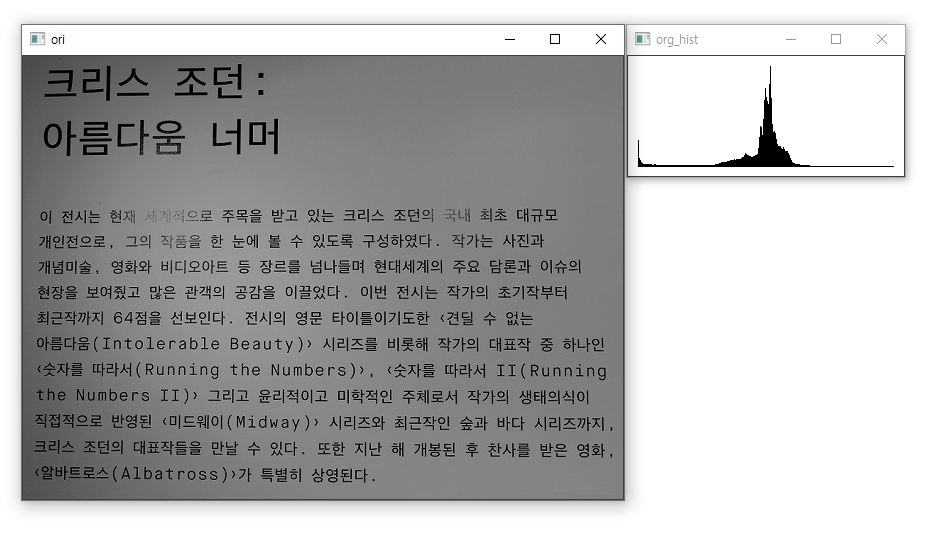
왼쪽의 이미지는 8비트 600*443 사이즈의 영상이고, 오른쪽은 왼쪽 영상의 히스토그램입니다. Gray level값 0(글자) 근처에 조금 모여있고, Gray level값 132(배경)를 중심으로 퍼져있는 양상을 띕니다.
1) Gray level(pixel intensity) 별 확률 구하기
- Gray Level의 범위는 $[1, 2, cdots, L]$ 으로 정의합니다. 8비트일 때는 1~256이 되겠지요.
- 각 Gray level별 픽셀의 개수를 셀 때는 $n_i$으로 정의합니다.
즉, 각 Gray level 별 픽셀 수를 더하면 전체 픽셀의 수($N$)가 나옵니다.
$$N = n_1 + n_2 + cdots + n_L$$
※ 위 영상의 전체 픽셀수($N$)는 265,800입니다.
Gray level이 0인 픽셀수($n_0$)는 4,090개, Gray level이 132인 픽셀수($n_{132}$)는 15,863개입니다.
각 Gray level의 확률(probability)을 구해보도록 하겠습니다. 예를 들어 Gray level이 132인 픽셀은 15,863개라고 하였으므로, 이를 전체 픽셀로 나눠주면 0.0597이 나옵니다. 결국 Gray level 별 픽셀의 확률을 전부 더하면 1이 됩니다.
$$p_i = n_i/N, (p_i geq 0)$$
$$sum_{i=1}^{N} p_i = 1 $$
2) 그룹 나누기
이제 Gray level을 두 그룹으로 나눌 것입니다. 첫번째 클래스를 $C_0$, 두번째 클래스를 $C_1$이라고 정의하겠습니다. 그리고 찾고자 하는 최적의 임계값을 $k$라고 하겠습니다.
- $C_0$에 속하는 픽셀의 Gray level 범위는 $[1, cdots, k]$이고,
$C_1$에 속하는 픽셀의 Gray level 범위는 $[k+1, cdots, L]$ 입니다. - 특정 픽셀이 $C_0$ 또는 $C_1$에 속할지 확률을 계산합니다. 단순히 각 클래스에 속한 Gray level의 확률을 더하면 됩니다.
$$Pr(C_0) = sum_{i=1}^{k} p_i = omega(k) = omega_0$$
$$Pr(C_1) = sum_{i=k+1}^{L} p_i = 1-omega(k) = omega_1$$
3) 평균값 구하기
다음으로 각 클래스를 대표하는 Gray level의 값을 구해봅니다. 대표값은 평균이고 식은 아래와 같습니다.
$$mu_0 = sum_{i=1}^{k} i Pr(i|C_0)$$
$$mu_1 = sum_{i=k+1}^{L} i Pr(i|C_L)$$
위 식에 베이즈 정리를 적용하여 $Pr(i|C_0) = frac{Pr(C_0|i)Pr(i)}{Pr(C_0)}$으로 바꿔봅니다.
$$mu_0 = sum_{i=1}^{k} i frac{Pr(C_0|i)Pr(i)}{Pr(C_0)} $$
$$mu_1 = sum_{i=k+1}^{L} i frac{Pr(C_1|i)Pr(i)}{Pr(C_1)} $$
여기서 $Pr(C_0|i)$은 1입니다. 생각해보면 $i$는 항상 $C_0$ 출신이기 때문에 당연한 것입니다. 식을 정리해보면 다음과 같습니다.
$$mu_0 = frac{1}{omega_0} sum_{i=1}^{k} i Pr(i) = frac{mu(k)}{omega(k)} $$
$$mu_1 = frac{1}{omega_1} sum_{i=k+1}^{L} i Pr(i) = frac{mu_tau – mu(k)}{1-omega(k)} $$
$omega(k) $ 는 위에서 이미 설명을 했습니다. $mu(k)$는 1부터 레벨 k까지의 평균 Gray level 값을 의미하고, $sum_{i=1}^{k} ip_i $ 으로 구할 수 있습니다. 즉, 전체 이미지의 평균 Gray level 값은 다음과 같습니다.
$$mu_tau = mu(L) = sum_{i=1}^{L} ip_i$$
그러므로 다음과 같이 정리할 수 있습니다.
$$ omega_0 + omega_1 = 1 $$
이고,
$$omega_0mu_0 + omega_1mu_1 = omega(k)*frac{mu(k)}{omega(k)} + (1-omega(k))*frac{mu_tau – mu(k)}{1-omega(k)}= mu_tau$$
가 됩니다. 굉장히 긴 것 같지만, 아직 평균값 밖에 안 구했습니다.^^;
4) 분산 구하기
각 클래스의 분산을 구하면 다음과 같습니다.
$$sigma^2_0 = sum_{i=1}^{k}(i-mu_0)^2 Pr(i|C_0) = sum_{i=1}^{k} (i-mu_0)^2 p_i/omega_0 $$
$$sigma^2_1= sum_{i=k+1}^{L}(i-mu_1)^2 Pr(i|C_1) = sum_{i=k+1}^{L} (i-mu_1)^2 p_i/omega_1 $$
within-class의 분산은 $sigma^2_W$, between-class의 분산은 $sigma^2_B$, 전체 분산은 $sigma^2_T$라고 하겠습니다.
$$sigma^2_W = omega_0sigma^2_0 + omega_1sigma^2_1$$
within-class는 2차 적률이므로 연산이 다소 복잡하다는 단점이 있습니다. 연산을 좀 더 간단히 실시하기 위해 between-class 분산값을 제안합니다. 앞서 2) 3) 과정에서 구했던 값들을 활용하면 됩니다.
$$sigma^2_B = omega_0(mu_0 – mu_tau)^2 + omega_1(mu_1 – mu_tau)^2 = omega_0omega_1(mu_1 – mu_0)^2$$
$$=omega(k)(1 – omega(k)) (frac{mu_tau-mu(k)}{1-omega(k)} – frac{mu(k)}{omega(k)})^2 $$
$$=frac{(mu_tau omega(k) – mu(k))^2}{omega(k)(1-omega(k))}$$
드디어 최적의 임계값 $k$를 구하기 위한 식이 완성되었습니다. 이제 Gray-Level 값을 넣어서 between class가 최대가 되게 하는 $k$를 찾으면 됩니다.
참고로, 전체 분산과 관련된 식은 아래와 같습니다.
$$sigma^2_T = sum_{i=1}^{L} (i-mu_tau)^2 p_i$$
$$sigma^2_W + sigma^2_B = sigma^2_T$$
Otsu 알고리즘 적용 결과
Otsu 알고리즘을 굳이 직접 구현하지는 않을 것이고, OpenCV의 threshold 함수를 통해서 결과를 보여드리도록 하겠습니다. threshold 함수에 대한 설명은 이전 포스팅에서 소개하였습니다.
예제코드
#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main()
{
Mat src = imread("text.jpg", IMREAD_GRAYSCALE);
if (src.empty())
{
cerr << "file error" << endl;
return 1;
}
Mat dst;
threshold(src, dst, 0, 255, THRESH_BINARY|THRESH_OTSU);
imshow("src", src);
imshow("dst", dst);
waitKey();
destroyAllWindows();
return 0;
}실행 결과

글자와 배경이 어느 정도 구분이 되지만, 왼쪽 상단 부분은 글자가 잘 보이지 않아 다소 아쉽습니다. 전체 영상에서 고정된 임계값을 사용하면 이러한 문제를 해결하기 어렵습니다. 그래서 다음 포스팅에서는 이 문제를 해결하기 위한 방법을 제시하도록 하겠습니다.
